Source: Smart Car Tech

In the realm of autonomous driving, the lateral control algorithm serves as the driver's hands, dictating whether the vehicle can accurately follow a predetermined path. Among the various lateral control algorithms, the Pure Pursuit algorithm stands out due to its simplicity and effectiveness, particularly in low-speed scenarios such as logistics vehicles in parks and autonomous parking. Today, we will demystify this algorithm using simple language: how does it mimic human driving? What pitfalls should be avoided during implementation? And in which scenarios is it most suitable?

From Human Driving to Algorithm: Pure Pursuit's 'Imitation Show'

When humans drive, they do not fixate on the car's front but rather look ahead at a target point and naturally turn the steering wheel to align with it. The Pure Pursuit algorithm 'mathematizes' this process.

First, 'slim down' the car: Simplification from four wheels to two wheels

While the turning principle of a real car is complex (e.g., Ackermann steering), the Pure Pursuit algorithm adopts a simpler 'bicycle model':

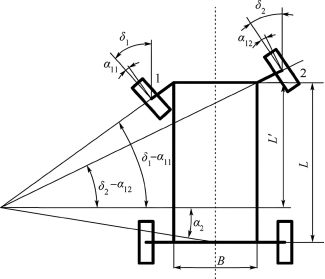
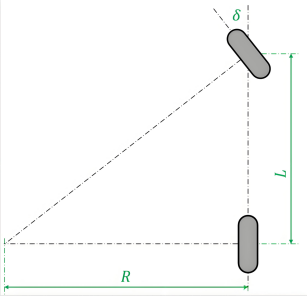
Figure: Ackermann steering geometry of a real vehicle (top) and its simplified bicycle model (bottom)

By simplifying the car into 'two wheels' (one for the front axle and one for the rear axle), and considering only planar motion, the relationship between the front wheel angle δ and the turning radius R becomes straightforward: tan(δ) = wheelbase L / turning radius R.

In other words, once the target turning radius R is calculated, the required steering wheel angle (δ = arctan(L/R)) can be directly obtained.

This model performs exceptionally well in low-speed scenarios below 60 km/h, with lateral deviation controlled within 15 cm (about the width of a fist).

Core Operation: Focus on the Target Point and Draw an Arc to Approach It

The Pure Pursuit algorithm works much like a novice driver practicing:

Select the target point: Starting from the rear axle, find a 'preview point' (ld meters ahead) along the planned route.

Calculate the turning radius: Determine the radius of the arc needed to travel from the current position to the target point.

Turn the steering wheel: Use the formula to calculate the angle the front wheel should turn based on the arc radius.

The entire process is akin to drawing a circle with a compass – the rear axle as the center, the preview distance ld as the radius, and the target point as a point on the circle.

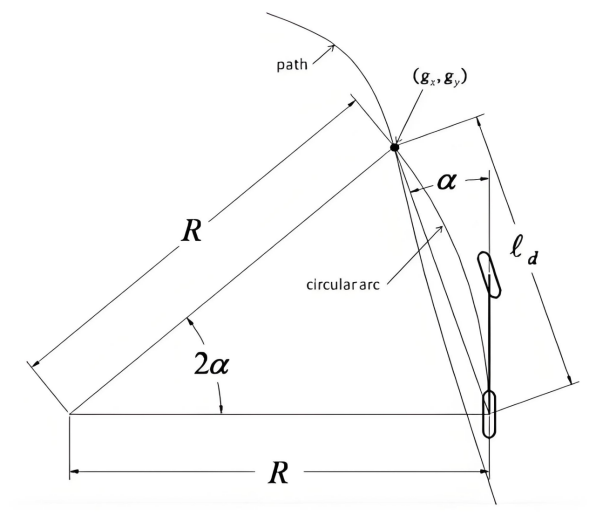
Figure: Geometric relationship derivation of the Pure Pursuit algorithm

Engineering Implementation: Turning Formulas into 'Runnable Code'

While the theory is straightforward, implementation hides many details. We will break down the key operations step by step according to the algorithm's operation steps.

Step 1: Locate the Target Point

The planned route's coordinates are in the 'global map' (e.g., latitude and longitude), while the vehicle needs the target point's position in its 'own coordinate system' (e.g., '5 meters ahead, 0.3 meters to the right'). This requires coordinate transformation:

In simple terms, it converts the 'point on the map' into a 'position relative to oneself' to clearly calculate whether to turn left or right.

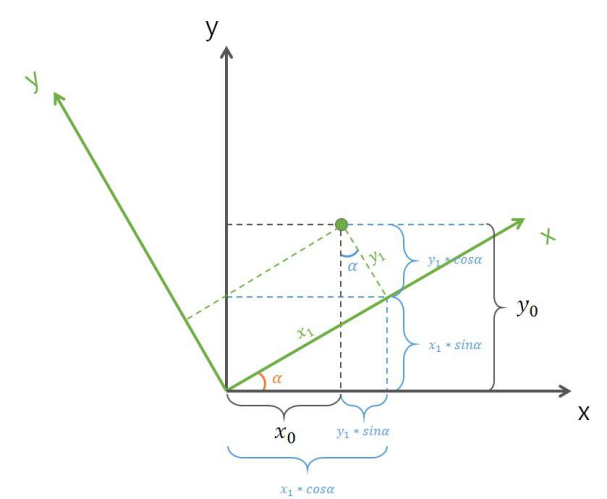
Figure: Coordinate transformation

Step 2: How to Determine the Preview Distance?

The preview distance ld (how far ahead to look) is a critical parameter that directly affects the control effect:

Very slow vehicles (e.g., < 5 km/h during parking): Look 1-2 meters ahead.

Vehicles in parks (30-40 km/h): Look 3-5 meters ahead.

Faster speeds? Sorry, the Pure Pursuit algorithm is not adept at handling them (reasons will be explained later).

A commonly used speed-adaptive strategy in engineering: The faster the speed v, the farther the preview distance ld (e.g., ld = k × v, with k ranging from 1.1 to 1.5). But note:

Convert the speed unit to m/s (the CAN bus often gives km/h, don't forget to divide by 3.6).

Leave a minimum preview distance of 3-5 meters (to prevent errors when the speed is 0).

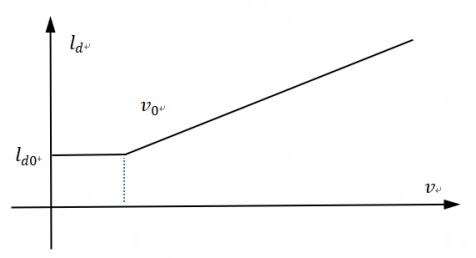
Figure: Relationship between preview distance and speed

Step 3: How to Select the Target Point? Don't Get It Wrong!

When selecting the target point, find the point that 'just exceeds the preview distance ld'. The steps are simple:

1. First, find the point closest to oneself on the planned route (equivalent to the 'current position').

2. Count forward from this point, accumulating the route length until it exceeds ld, and this point is the target point.

Final Step: How to Calculate the Steering Wheel Angle? What Additional Processing is Needed?

With the target point, directly calculate the front wheel angle using the following formula:

Steering angle δ = arctan(2 × wheelbase L × sin(α) / preview distance ld)

(α is the angle between the vehicle's current heading and the direction of the target point, calculated using locally transformed coordinates).

However, during implementation, two additional steps are required:

Convert to steering wheel angle: Front wheel angle × steering gear ratio (e.g., a ratio of 16 means the steering wheel turns 16 degrees for every 1-degree turn of the front wheel).

Smoothing: Use a first-order low-pass filter to eliminate jitter (e.g., filter coefficient 0.2, new angle = 0.8 × old angle + 0.2 × calculated value).

Pure Pursuit Algorithm: Which Scenarios are 'Usable' and Which are 'Troublesome'?

Advantages: Simplicity is King

Fast calculation: Single-frame processing < 5 ms, runnable on ordinary microcontrollers.

Robustness: Small positioning errors (e.g., 10 cm) do not affect performance.

Few parameters: Mainly adjust 2-3 parameters related to the preview distance, accessible even for beginners.

Disadvantages: Not Suitable for High-speed Scenarios

Ignores dynamics: Does not consider tire slippage (e.g., on wet roads, the calculated steering angle may be inaccurate).

Prone to deviation at high speeds: Stability decreases significantly above 60 km/h (sharp turns tend to 'cut corners').

Parameter sensitivity: A 1-meter difference in preview distance can lead to vastly different control effects.

Most Suitable Scenarios

Low-speed park vehicles: Delivery vehicles in factories and campuses (speed < 40 km/h).

Autonomous parking: Parking scenarios within 10 km/h, where short preview distances enable precise parking.

Agricultural machinery: Linear operations in farmland, combined with PID compensation to improve accuracy.

Engineering Implementation Pitfall Avoidance Guide

The preview distance is not the bigger, the better:

Low speed (< 20 km/h): 3-5 meters.

Medium speed (20-40 km/h): 5-8 meters.

Sharp turns: 20% shorter than on straight roads (to prevent cutting corners).

Don't adjust filter parameters randomly:

Use strong filtering for jitter suppression (coefficient 0.1-0.3).

Use weak filtering for high-speed scenarios (coefficient 0.5-0.8) to avoid response lag.

Don't ignore unit conversion:

Speed unit: km/h → m/s (divide by 3.6).

Angle unit: Radians → degrees (the algorithm calculates in radians, but the CAN bus sends in degrees).

The 'Survival Wisdom' of Simple Algorithms

The Pure Pursuit algorithm is akin to the 'old ox' in autonomous driving – not the most advanced but winning with its simplicity and reliability. In low-speed enclosed scenarios, its performance is even comparable to complex Model Predictive Control (MPC).

Understanding its principle not only helps you quickly implement a usable lateral control module but also reveals that a good algorithm is not necessarily the most complex but one that effectively solves problems in specific scenarios.

Next time you ride in a driverless vehicle in a park, observe its route around corners – you might just see the 'shadow' of the Pure Pursuit algorithm.

- End -

Disclaimer:

Any works on this public account that indicate 'Source: XXX (not Smart Car Tech)' are reproduced from other media. The purpose of reproduction is to deliver and share more information and does not represent the platform's endorsement of the views or responsibility for their authenticity. The copyright belongs to the original author. Please contact us if there is any infringement to delete the content.